浅谈Manacher算法在OI中的应用&CSP赛前总结——by WKAHPM

发表于 | 更新于 | 评论数： | 阅读次数：
本文字数： 3.1k | 阅读时长 ≈ 3 分钟

0.什么是Manacher

Manachar算法主要是处理字符串中关于回文串的问题的，它可以在 O（n） 的时间处理出以字符串中每一个字符为中心的回文串半径——摘自百度百科

1.从暴力谈起

先看一道例题洛谷P3805

题意十分简单明了，求一个字符串$S$中的最大回文子串长度

很容易想到一种$O(N^3)$算法，枚举子串的左边界$l$右边界$r$,判断该子串是否回文即可。

1
2
3
for(int l = 0; l < len; l ++)
  for(int r = l; r < len; r ++)
    if(check(l , r)) ans = max(ans , r - l + 1);

在此算法上加入亿一点简单优化可以优化到$O(N^2)$,对于长度为奇数的回文字符串，回文子串的中心一定是某个字符，对于长度为偶数的回文字符串，回文子串的中心一定是两个字符之间的空隙，一种显然的作法是枚举这些回文中心，向两边拓展直到字符不相等或到达边界

由于$WKAHPM$比较懒,所以就不贴代码了。

暴力的缺点：

  • 1.需要分类讨论
  • 2.枚举了很多没用的子串

这时候我们就需要再加入亿一点优化。

2.Manacher的初始化

暴力的缺点——需要分类讨论

如何解决这个问题？一种作法是在每个字符之间再加入一个分隔字符（当然这个字符不能存在在原本的字符串中），举个栗子,比如字符串$ababac$：

a b a b a c
# a # b # a # b # a # c #

这个方法有效地避免了分类讨论，容易发现我们插入了$N+1$个#号，字符串的长度变为$2N+1$，为奇数，是不是很神奇呢

为了防止越界情况，我们在开头和结尾再加入一个字符，比如$@$，这部分的代码可以这么写

1
2
3
4
5
6
7
8
9
10
void news()
{
	s_new += "@#";
	for(int i = 0;i < s.size(); i++)
	{
		s_new += s[i];
		s_new += '#'; 
	}
	s_new += '@';
}

3.Manacher的原理

定义$p[i]$表示以$i$为对称中心能扩展的最大回文子串半径，即左/右边界到对称中心的距离。

$Manacher$的算法思想就是快速求出$p$数组。

我们来看看$p$数组与答案的关系(这里省略@)

s # a # b # a # b # a # c #
ans 0 1 0 3 0 5 0 3 0 1 0 1 0
p 1 2 1 4 1 6 1 4 1 2 1 2 1

显然有$ans[i]=p[i]-1$

证明：

设回文子串$s$原来的长度为$len$，对称中心为$i$；

则$s$插入字符后的长度变为$2\times len+1$；

此时$p[i]=(2\times len+1+1)/2=len+1$,所以$p[i]-1$即为答案

所以求出$p[i]$就可以求出答案

4.Manacher的实现

$Manacher$的实现用到了回文子串的一个性质——对称性

利用该性质可以有效地避免重复枚举，通过之前枚举过的子串来确定这个点至少能扩展的长度

设$mr$为之前找到的回文子串的最右边，$mid$为该回文子串的对称中心。

假设当前枚举到第$i$位，因为枚举过$mid$了，所以显然有$i>mid$，接下来需要分类讨论两种情况来快速求出$p[i]$：

为了方便讨论，设$j$为$i$以$mid$为对称中心的对称点，$s_{i}$是以$i$为对称中心的回文子串，$s_{j}$是以$j$为对称中心的回文子串

(1)i < mr

这时候我们又能分2种情况

  • 1 $s_{i}$的右边界不大于$mr$

如图

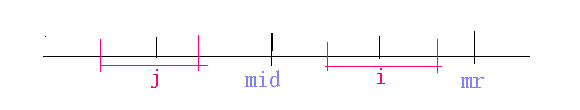
TIM截图20191115112913.png

由对称性知，此时$p[i]=p[j]$

  • 2 $s_{i}$的右边界大于$mr$

如图

TIM截图20191115132136.png

这时我们只能确定α段是具有对称性的，此时$p[i]=mr-i$

也就是说，当$i$在$mr$左边，那么$p[i]$肯定是$mr-i$与$p[j]$的最小值。因为$j$与$i$关于$mid$对称，所以在$[i,mr]$这一段内可以直接使用$p[j]$的值，但是$i$已知的回文串长度不能到$mr$后面去，所以跟$mr-i$取$min$。

(2) i >= mr

此时我们无法通过对称性得到$p[i]$，所以$p[i]=1$

代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
int Manacher()
{
	int mx=0;
	int maxn=-1;
	int id=0;
	for(int i=1;i<s_new.size();i++)
	{
		if(i<mx)//情况1
		  ans[i]=min(ans[2*id-i],mx-i);
		else//情况2
		  ans[i]=1;
		while(s_new[i-ans[i]]==s_new[i+ans[i]]) ans[i]++;//扩展
		if(mx<i+ans[i])//更新右边界
		{
			id=i;
			mx=i+ans[i];
		}
		maxn=max(maxn,ans[i]-1);//更新答案
	}
	return maxn;
}

5.例题

洛谷P5018对称二叉树

这题可以用$Manacher$来解决。

可以先用中序遍历对每个节点编号，利用$a$和$size$数组存放每个节点的权值和以这个节点为根节点的二叉树的节点数，对每个数组进行$Manacher$，将先后两次的以第$i$个点为对称中心的最大回文子串半径存放在$p1[i],p2[i]$中。

另外本题不需要初始化，$Manacher$初始化的原因是可能存在偶数长度的回文子串，但在对称二叉树中不可能存在偶数长度的回文子串，因为在对称二叉树中，除根节点以外每一个左儿子都有一个右儿子与之对应，所以节点数为奇数个。

求出$p1,p2$后，枚举编号$1$~$N$，判断以$i$为根节点的二叉树是否为对称二叉树，如果是则对$ans$和$size[i]$取$max$，对称二叉树需要满足两个条件：

  • 1 权值对称

  • 2 结构对称

体现在程序中就是$p1[i] \times 2 - 1 >= size[i]$并且$p2[i] \times 2 - 1 == size[i]$

首先解释一下为什么是$p1[i] \times 2 - 1$而不是$p1[i]-1$

$p1[i] \times 2 - 1$是因为之前的$Manacher$我们没有进行初始化，所以此时的$p1[i]$要乘2

接着解释一下为什么是$p1[i] \times 2 - 1 >= size[i]$

如图

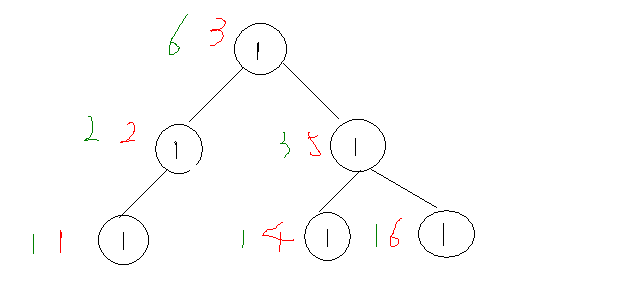
TIM截图20191115154337.png

如果写成$p1[i] \times 2 - 1 == size[i]$的话，则对于编号为$5$的节点，$p1[5] \ times 2 - 1 =5$,而$size[5]=3$，所以当节点权值相等时，可能出现$p1[i] \times 2 - 1 > size[i]$的情况。

6.结语

明天就是$CSP$了，大家调整好心态，多背背模板，基本上$t1t2$过了$t3t4$打一下暴力就省一了，祝各位$RP++$(这不是毒奶)

愿TIM截图20191115171839.png降临到你身边