浅谈OI中的骗分技巧——by WKAHPM

发表于 | 更新于 | 评论数： | 阅读次数：
本文字数： 5.5k | 阅读时长 ≈ 5 分钟

0.写在前面

在NOIP$CSP$的考场上，很多题目我们在考场上往往无法想到正解（当然大佬除外）。这时候我们就需要一些骗分技巧来为自己争取一些部分分。

1.骗分的意义

首先我们要了解什么是子任务。

对于一道题，它可能存在多个子任务。这些子任务的数据往往具有某些特点或者在某个小范围内，骗分的意义就是在打不出正解的情况下拿到这些子任务的分数。

例如$2018NOIP$ $T2$中的龙虎斗，它的子任务分布是这样的

【数据规模与约定】

$1 < m < n,1 ≤ p1 ≤ n.$

对于$20$%的数据,$n = 3, m = 2, ci = 1, s1,s2 ≤ 100$.

另有$20$%的数据,$n ≤ 10, p1 = m, ci = 1, s1,s2 ≤ 100$.

对于$20$%的数据,$n = 3, m = 2, ci = 1,s1,s2 ≤ 100$.

对于$60$%的数据,$n ≤ 100, ci = 1,s1,s2 ≤ 100$.

对于$80$%的数据,$n ≤ 100, ci,s1,s2 ≤ 100$.

对于$100$%的数据,$n ≤ 10^5, ci = 1, s1,s2 ≤ 10^9$.

观察可以发现,$80$%的数据都很小，这时候我们就可以用暴力来拿到这$80$分。

2.基础的骗分

1.输样例

一道题目都会给你输入输出样例，如果你想不出其他解决该问题的方法，可以尝试直接输出样例，这就是考验你$rp$的时候了

例题：$2018NOIP$ $T4$对称二叉树

输出第二个样例即$3$可以拿到32分

没错就是这段代码可以为你拿到32分

1
2
3
4
5
6
7
8
9
10
11
#include <bits/stdc++.h>
using namespace std;

int main() {
    //freopen("tree.in", "r", stdin);
    //freopen("tree.out", "w" ,stdout);

    cout << 3;

    return 0;
}

当一道题目包含无解的情况时，也可以通过输出无解来获得部分分

2.输出随机数

这个也是考验$rp$的，根据数据范围输出随机数。

随机数生成代码

1
2
3
4
5
6
7
8
9
#include<bits/stdc++.h>
using namespace std;

int main()
{
	srand(time(0)); //随机种子
	printf("%d" , rand()%b + a) //输出一个范围在a~a+b-1的随机数 
	return 0;
}

需要注意的是随机数的生成范围在不同操作系统下是不一样的，在Windows下是$0$~$32767$

由于篇幅限制，基础的骗分技巧不再赘述。

3.高级骗分技巧

1.打表

很多人可能认为打表是最基础的骗分技巧，但是打表也是有艺术的。

打表的用处很多，例如

  • 1 减小时间复杂度

  • 2 找规律

  • 3 ······

先说说如何减小时间复杂度。

当一些题目数据范围很小时，我们可以考虑通过打表使程序运行效率提高，例如$2008NOIP$ $T3$传球游戏

这是我$90$分的程序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include<bits/stdc++.h>
using namespace std;
int f[31][31],n,m;
int dfs(int x,int y)
{
	if(f[x][y]) return f[x][y];
	if(y==0) 
	{
		if(x==1)return f[x][y]=1;
		else return f[x][y]=0;
	}
	if(x==n)
	{
		return f[x][y]=dfs(x-1,y-1)+dfs(1,y-1);
	 } 
	else
	  if(x==1) return f[x][y]=dfs(n,y-1)+dfs(x+1,y-1);
	  else
	    return f[x][y]=dfs(x-1,y-1)+dfs(x+1,y-1);
}
int main()
{
	scanf("%d%d",&n,&m);
	printf("%d",dfs(1,m));
	return 0;
}

但是这个程序会被$10$ $29$这个数据给卡超时

这个时候加入打表就可以完美$AC$这道题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include<bits/stdc++.h>
using namespace std;
int f[31][31],n,m;
int dfs(int x,int y)
{
	if(f[x][y]) return f[x][y];
	if(y==0) 
	{
		if(x==1)return f[x][y]=1;
		else return f[x][y]=0;
	}
	if(x==n)
	{
		return f[x][y]=dfs(x-1,y-1)+dfs(1,y-1);
	 } 
	else
	  if(x==1) return f[x][y]=dfs(n,y-1)+dfs(x+1,y-1);
	  else
	    return f[x][y]=dfs(x-1,y-1)+dfs(x+1,y-1);
}
int main()
{
	scanf("%d%d",&n,&m);
	if(n==10&&m==29) 
	{
		cout<<0;
		return 0;
    }
	printf("%d",dfs(1,m));
	return 0;
}

这段程序比上一段程序多出来的部分就是

1
2
3
4
5
if(n==10&&m==29) 
	{
		cout<<0;
		return 0;
    }

对于一些对素数判断存在要求的题目，我们可以预处理出素数表，减少判断的时间。

大致是这样的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include<bits/stdc++.h>
using namespace std;
  
bool prime(long long num) //快速判断素数
{
	if (num == 2 || num == 3)
	{
		return true;
	}
	if (num % 6 != 1 && num % 6 != 5)
	{
		return false;
	}
	for (int i = 5; i*i <= num; i += 6)
	{
		if (num % i == 0 || num % (i+2) == 0)
		{
			return false;
		}
	}
	return true;
}
                              
int main()
{
   freopen("prime.out","w",stdout);//将表输出到文件里，方便复制
	for(int i = 2; i <= n; i ++)
      if(prime(i)) cout << "i,"//加入逗号方便复制
	return 0;
}

这时候将prime.out里的数字复制到表里就可以了

1
Prime[LEN]={2,3,5,···}

再来说说找规律。

对于一些题目，我们可以输出一些小数据的答案，观察答案与输入数据的关系，这种方法一般适用于数论题。

如$1999NOIP$ $T1$? Cantor表

可以通过行列和答案的关系找出某种规律。

打表的方式千变万化，所以有着”打表出省一”之说（笑），当然也不能过分依赖打表，造成思维惰性。

你的NOIP.png

2.dfs

如果你熟练掌握了$dfs$（深度优先搜索），你会发现“万物皆可搜”。

当一个题目打不出来怎么办？先打个$dfs$，可能这不是最优解，但是$dfs$思路清晰，码量小，可以拿到部分分。而且有时它也可以便于你想出正解。动态规划的思想有部分就来自于搜索。

例如$2018NOIP$ $T4$对称二叉树

如果你熟练掌握了二叉树的知识，你会很容易写出一个$dfs$，而$dfs$就是这道题目的正解。。。

所以万物皆可搜 万物皆可搜 万物皆可搜

3.灵活运用子任务的数据范围或数据特点

数据范围往往不是无意义的，它存在的意义就是卡掉某些错解。

先上张图

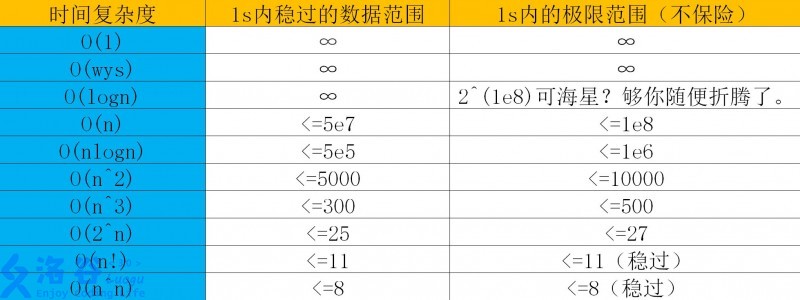
时间复杂度.png

数据范围对选择算法非常重要，算法的选择将会决定你是否能做出这道题。

根据子任务的数据范围，我们可以通过它来选择不同子任务用的算法。

如开头提到的龙虎斗，对于$80$分的数据$n<=100$,用$O(n^2)$的算法是肯定不会超时的。所以可以这么写代码

1
2
3
4
5
6
7
8
if(n <= 100)
{
   ····//暴力代码
}
if(n > 100)
{
  ····//瞎搞
}

比如$2018NOIP$ $T3$摆渡车

对于$10$%的数据，满足$m=1$

这时意味着每个人的等待时间都为0，所以

1
2
3
4
5
if(m == 1)
{
    cout << 0 ;
    return 0;
}

就可以拿到10分

4.对拍

在你写出骗分程序后，如果你所有题目都做完了且检验后，这时你就可以返回之前通过骗分做的题目，想一些正解。

还是以龙虎斗为例，在你打出一个可以满足$100$%数据范围的时间复杂度的程序后，你想检验它的正确性，这时候运用对拍可以十分方便地检验。

对拍模板：

1
2
3
4
5
6
7
:loop
shuju.exe
baoli.exe
shiyan.exe
fc fan.out fan1.out
if %errorlevel%==0 goto loop
pause

新建一个.txt文件，将上面的代码复制进去。再将后缀名改为.bat，文件名任意。

其中shuju.exe是你出数据的程序，shiyan.exe是你想的“正解”，baoli.exe是你打的暴力程序。

fan.out和fan1.out分别是你baoli和shiyan的输出文件。

这些东西需要放在同一个文件夹里，然后双击这个文件名.bat就可以开始愉快的对拍了。

5.例题

1.最大连续和

首先看到$10$%的数据所有数都是正数，这是只要把所有数加起来就是结果。

对于$30$%的数据，我们很容易可以写出一个暴力。

1
2
3
4
5
6
7
8
9
10
ans = a[1];
	for(int i = 1; i <= n; i ++)
	  for(int j = i; j <= n; j ++)
	  {
	  	int sum = 0;
	  	for(int k = i; k <= j; k ++){
	  		sum += a[k];
		  }
		ans = max(ans , sum);
	  }

对于$50$%的数据，在$30$%的程序基础上加入前缀和优化。

对于$80$%的数据，可以考虑进行二分（数据过水，在洛谷上被水过去了）

对于$100$%的数据，定义$dp[i]$为$1$~$i$的最大连续和。

对于$a[i]$，明显有两种选择，一种是取之前的最大连续和，一种是不取之前的最大连续和，以这个数为开头。

1
dp[i] = max(a[i] , dp[i - 1] + a[i]);

2.$2017NOIP$ $T4$ 跳房子

首先观察题目，发现题目中存在无解的情况，所以可以先加入特判是否存在答案。判断条件就是所有格子的最大和未超过$k$的话，输出无解。

接下来观察数据范围，发现$1,2$组数据$n$的范围较小，可以考虑$dfs$(见题目目录下1.cpp)

可以在该程序的基础上加上二分进行优化(见题目目录下2.cpp)

继续观察数据范围，发现前$5$组数据$n<=500$，可以考虑用朴素$dp$求解

定义$dp[pos]$为从起点到$pos$格能获得的最大分数，

不难发现$dp[pos]$可以由某个格$i$跳$j$步到达

所以有方程$dp[pos]=max(dp[pos],dp[i]+s[i+j])$

其中$0<=i<n,left<=j<=right,pos = i + j$，$left,right$分别是能跳的步数的左边界和右边界。时间复杂度$O(n^2)$（见题目目录下3.cpp）

这样本题就可以拿到$50$分了

如果想拿到满分需要加入单调队列优化$dp$，这里不再赘述（其实是我不会）

6.总结

骗分是种艺术，在考场上灵活运用骗分技巧可以为你争取部分分。但是这并不意味着你不用去思考这道题目的正解，要知道思考正解远比想尽办法骗分更有意义。