1.什么是LCA
LCA(Least Common Ancestors),即最近公共祖先,是指在有根树中,找出某两个结点u和v最近的公共祖先。——百度百科
这么说可能不直观,我们通过一张图来理解一下
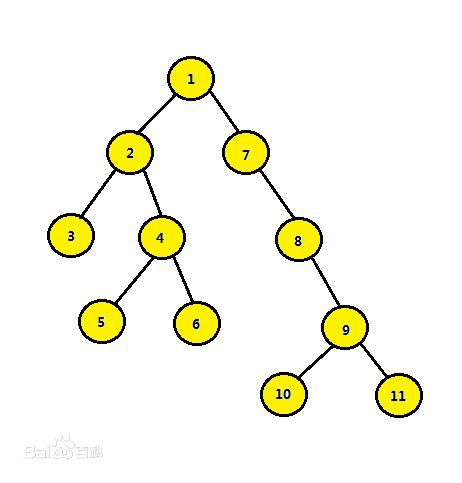
(图片来源百度百科)
在这棵树中,点$3$和点$6$的最近公共祖先是$2$,因为3的祖先是{1,2},6的祖先是{4,2,1}。它们的公共祖先是{2,1},而其中深度最大的是$2$
2.怎么求LCA
1.朴素算法
了解了$LCA$的定义,不难得出一种暴力算法,即对于$u,v$两个点,我们让它们不断地一步一步往上跳,直到第一次相遇。
算法时间复杂度:$O(N)$
2.倍增算法
既然一步一步跳太慢,我们可以考虑设计一种倍增算法,让它一次跳$2^{0},2^{1},···.2^{n}$次方步。
算法流程:
定义$fa[i][j]$为第$i$个点跳$2^{j}$步后达到的点,$deep[i]$为第$i$个点的深度。
1.建树,计算深度,预处理$fa[i][0]$
这一部分可以用$dfs$实现
1 | void dfs(int t , int father) //t表示当前点编号,father表示它的父亲结点编号 |
2.预处理$fa[i][j]$
因为$2^{j}=2^{j-1}+2^{j-1}$,所以我们可以得到转移方程
$fa[i][j]=fa[fa[i][j-1]][j-1]$
即先跳$2^{j-1}$到达$fa[i][j-1]$,再跳$2^{j-1}$步到达$fa[fa[i][j-1][j-1]]$
Code
1 | void prework() |
3.求$LCA$
假设求$x,y$的$LCA$
为了方便讨论,假设$deep[x]>deep[y]$,即$x$的深度大于$y$的深度
先让$x$跳到与$y$同一深度,代码如下
1 | for(int i = 20; i >= 0; i --) if(deep[fa[x][i]] >= deep[y]) x = fa[x][i];//只要x还比y深,就跳,否则不跳 |
如果这时候如果$x$已经等于$y$了,直接输出即可。
到达同一深度后,我们开始让$x,y$一起跳,注意这里我们要跳到的是它们$LCA$的下一层(因为我们跳到的是满足$x$和$y$不相等的最浅的一层,而它们的上层即为$LCA$)。
还是看最开始的例子,$3,6$,调整至同一高度后为$3,4$,,循环过后$x$和$y$的值并没有改变,因为我们跳到的是$LCA$的下一层。
代码如下
1 | for(int i = 20; i >= 0; i --) |
最后的答案就是$f[x][0]$了
完整代码1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
using namespace std;
int n , m , s , cnt;
int deep[500100];
int fa[500010][31];
struct G{
int to , Next;
}edge[1000010];
int head[500010];
void add(int from , int to)//建边
{
edge[++ cnt].Next = head[from];
edge[cnt].to = to;
head[from] = cnt;
}
void dfs(int t , int father)//预处理深度
{
deep[t] = deep[father] + 1;
fa[t][0] = father;
for(int i = head[t]; i ; i = edge[i].Next)
{
if(edge[i].to != father)
dfs(edge[i].to , t);
}
}
void prework()//预处理fa数组
{
for(int j = 1; j <= 20; j ++)
{
for(int i = 1; i <= n; i ++)
{
fa[i][j] = fa[fa[i][j - 1]][j - 1];
}
}
}
int query(int x , int y)//求LCA
{
if(deep[x] < deep[y]) swap(x , y);//令x的深度大于y的深度
for(int i = 20; i >= 0; i --) if(deep[fa[x][i]] >= deep[y]) x = fa[x][i];//让x,y跳到同一深度
for(int i = 20; i >= 0; i --) if(fa[x][i] != fa[y][i]) x = fa[x][i] , y = fa[y][i];//让x,y一起跳
if(x == y) return x;
else return fa[x][0];
}
int main()
{
// ios::sync_with_stdio(false);
scanf("%d%d%d" , &n , &m , &s);
for(int i = 1; i <= n - 1; i ++)
{
int x , y;
scanf("%d%d" , &x , &y);
add(y , x);
add(x , y);
}
dfs(s , 0);
prework();
for(int i = 1; i <= m; i ++)
{
int a , b;
scanf("%d%d" , &a , &b);
printf("%d\n" , query(a , b));
}
return 0;
}
时间复杂度$O(logn)$
4.一些思考
为什么求LCA中$j$要从大到小枚举。
这个和天平称重时从大到小放砝码有点类似,举个例子,比如跳9步,如果按从小到大枚举是$1+2+4+8$,而$9 \ne1+2+4+8$,还需要回去重新找,而从大到小的话直接求出$9=8+1$