题目描述

题解
首先考虑如何求树上的任意个点连通的边集的总长度的最小值
可以对树上的点进行一次$dfs$求出它们的$dfs$序,将所求点按$dfs$序排序后相邻两点(包括头尾)的距离之和即为使这些点连通的边集的总长度的最小值的两倍
如图(蓝色为各点$dfs$序)
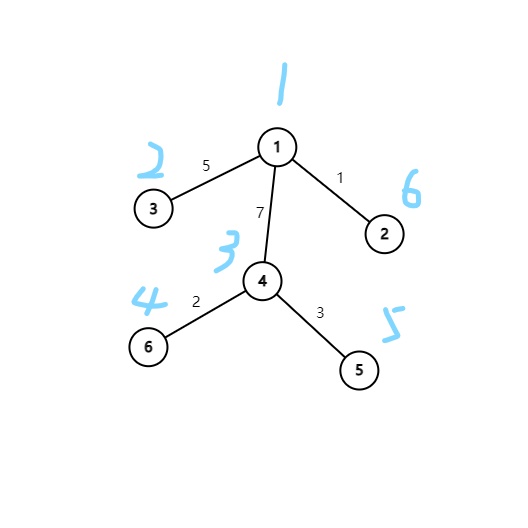
假设我们要让$1,2,3,5$连通
按$dfs$序排序后得到$1,3,5,2$
$dis(1,3)+dis(3,5)+dis(5,2)+dis(2,1)=5+15+11+1$
观察发现每条边都被计算两次,所以结果是答案的$2$倍
有了以上结论后,我们可以得出一个算法,使用平衡树或$set$维护所有异象石的$dfs$序,每次插入一个新的异象石$k$时,查找到它在已有异象石中的前驱和后继,假设为$i,j$,更新$ans$,令其减去$dis(i,j)$并加上$dis(i,k)+dis(k,j)$。同理,删除操作则令$ans$加上$dis(i,j)$减去$dis(i,k)+dis(k,j)$
注意特判边界
Code
1 |
|