0.问题类型
这是一道经典的最大子矩形问题,本人的思路参考了国家队wzk大佬的论文《浅谈用极大化思想解决最大子矩形问题》
这篇论文介绍了两种求最大子矩形的思路,分别是通过障碍点找子矩形和通过悬线找子矩形,本题的数据范围适合使用第一种方法
1.算法思路
定义极大子矩形为$4$条边都不能向外拓展的有效子矩形(这里的有效即子矩形内不包括障碍点)。
可以得到最大子矩形是所有极大子矩形中最大的,所以只要枚举最大的子矩形,求出其中最大的即可
2.算法实现
怎么找极大子矩形?根据极大子矩形的定义,我们可以得出极大子矩形的$4$条边一定覆盖障碍点(或边界)
为了方便讨论,我们先将整个牛场的4个顶点设为障碍点。
例如
10 10
4
1 1
3 4
6 3
9 8
1.从左往右搜
将障碍点按横坐标排序(左右顺序)后得到如下编号。
(作者画画不是那么好qwq)
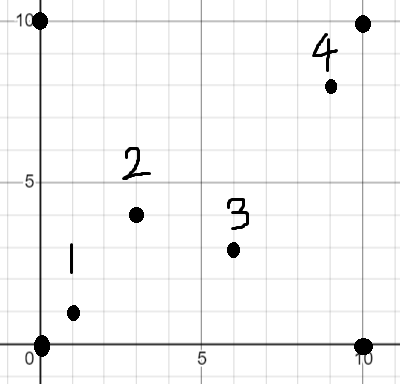
一开始从$1$号障碍点开始,从左往右找极大子矩形。
一开始的极大子矩形上下边界$up,low$为整个牛场的上下边界
$1$号障碍点往右找,到$2$号障碍点,如图
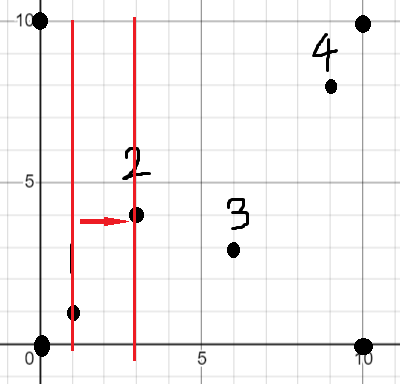
可以得到一个极大子矩形,它的面积就是障碍点$2$的横坐标减去障碍点$1$的横坐标乘以上边界减去下边界。
接下来需要对上下边界做一些修改,否则之后的极大子矩形可能会包括障碍点。因为$2$的纵坐标大于$1$的纵坐标,所以修改上边界,修改为$2$的纵坐标。
接下来到$3$,同理可以得到如下极大子矩形
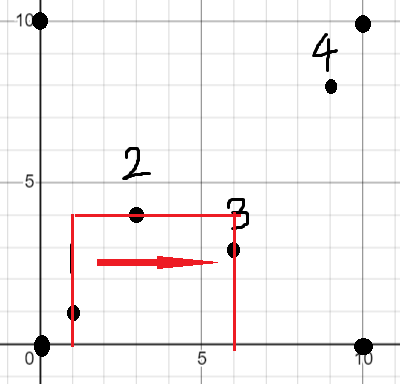
它的面积就是$3$的横坐标减去$1$的横坐标乘以上边界($2$的纵坐标)减去下边界
之后的$4$也同理。
然后从$2$开始往右找,从$3$开始往右找,从$4$开始往右找,跟从$1$开始找都是一样的。
2.从右往左搜
从左往右搜后我们会发现有一些遗漏的情况,就是极大子矩形的左边界是牛场的左边界,右边界覆盖一个障碍点的情况,如图
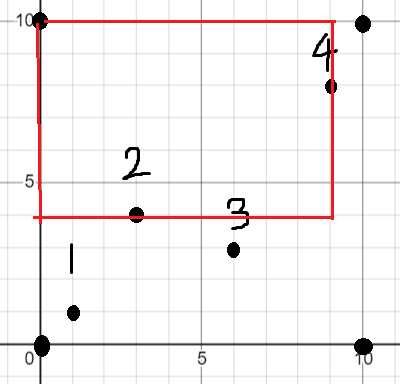
解决方法很简单,把从左往右搜倒过来从右往左搜一遍即可
3.特殊情况
在从左往右搜和从右往左搜后我们发现还有一种情况没有考虑到,就是极大子矩形的左右边界分别是牛场的左右边界,如图
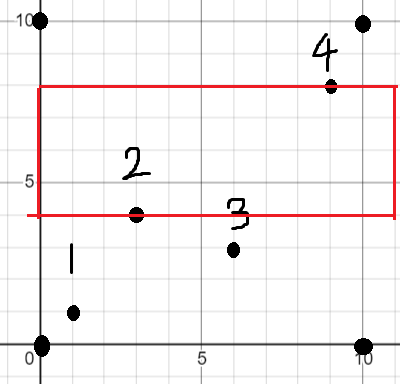
解决方法是,再将障碍点按纵坐标排序,如图
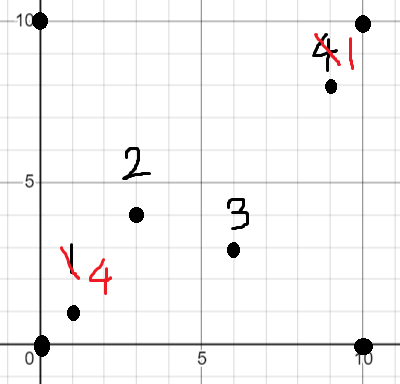
可以得到这类极大子矩形的面积就是相邻两个障碍点(按纵坐标排序后)纵坐标之差乘以牛场的长
时间复杂度$O(N^2)$,$N$为障碍点数
3.代码实现
1 |
|